
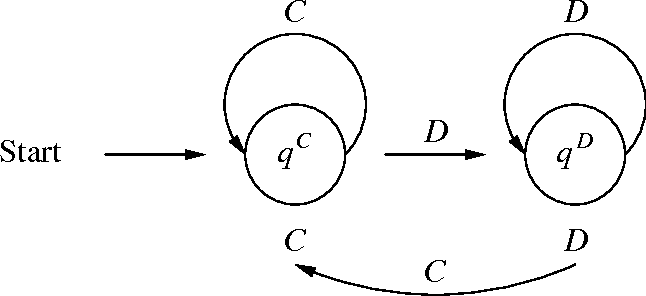
Latex Finite State Automata Series Of Blog
Such a multiplication should not be done according to the schoolbook, but just by subtracting n from 10000n. Suddenly today's guest list becomes clearer. Already guessed?-Yes?-No?-Then, here is the answer.Suppose that we want to multiply a huge number n by 9999. As I mentioned before, I am writing a series of blog posts on my Theory of Computation class.This particular post will be somewhat image-heavy due to complete lack of experience on how to use LaTeX in accordance with state machine diagrams.Ladies and Gentlemen, let me introduce you to the first guest of this opening ceremony: the equationYou might ask now: Why?-Why exactly this?-A small hint: It has to do with multiplication as the title of the first act says. In this context, the FSM is often directly related to a regular expression, and the goal is feed strings into the FSM to see if they match a regular expression.Keywords: Transducer, automaton, non-adjacent form, Hamming weight, tutorialCS Theory Part 1 of 8: Finite Automata.
The lights go on again and we immediately see14 =1 * 16 + 0 * 8 + 0 * 4 - 1 * 2 + 0 * 1 = 0).sub.2]. Tonight they will perform in a special way, but they need help from their digit sibling = -1, which brings us to the following riddle: Write 14 in base 2 with the digits -1, 0 and 1 such that there are fewer nonzero digits than in the standard binary expansion.Our digit triplet needs only a moment to prepare a solution. Usually they are used when writing a number in standard binary expansion, for example14 =1 * 8 + 1 * 4 + 1 * 2 + 0 * 1 =. That is our cue to introduce the next guests: the digits 0 and 1.
A bunch of questions appear: So how do we determine such a digit expansion of a general number? Is there a way to simply get it from the binary expansion? Is this the best possible way to write an integer?Questions over questions-all of which will be answered after a short break.In this second act we will first meet the main characters of this article. It guarantees that no two adjacent digits are nonzero at the same time and the digit expansion (1) is indeed such a non-adjacent form. This brings us directly to the special guest of this evening, the non-adjacent form, which will be present in the whole article.
Some of these magic boxes can only be opened giving them a special digit expansion (see Section. You will find them everywhere. As a small side note, the authors Clemens, Daniel and Sara work with digit expansions a lot in their research, so these examples seem to be a natural choice.Back to business there are some presents for each of you-these little boxes over there called automata.


 0 kommentar(er)
0 kommentar(er)
